Introduction
The 8-Queens problem is a well-known puzzle in computer science and artificial intelligence. It involves positioning eight queens on an 8x8 chessboard in such a manner that no two queens can attack each other. In other words, no two queens should share the same row, column, or diagonal. This seemingly straightforward puzzle is a powerful example of problem-solving techniques and is often utilized to demonstrate different algorithms. In this blog, we will delve into solving the 8-Queens problem using local search algorithms, a class of optimization methods that incrementally refine a solution until a satisfactory one is achieved.
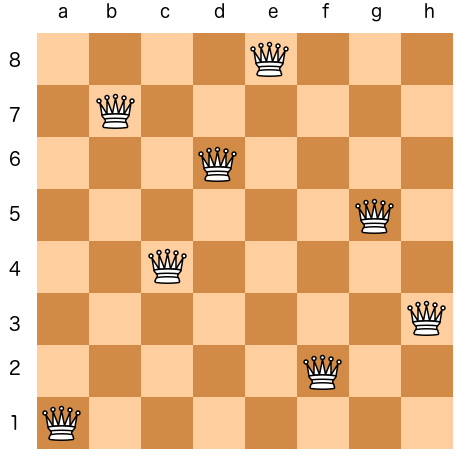
The 8-Queens problem is str aightforward. On an 8x8 chessboard, the queen can move any number of squares horizontally, vertically, or diagonally. Typically, there is one queen per side in the game, but for this puzzle, there are 8. This can also be extended to N queens on an NxN board. The objective is to arrange 8 queens on the board in such a way that no two queens threaten each other. In the image above, you can see that no queen is within the attack range of another. Here's an example of a board configuration that does not solve the puzzle:

The queens in the 4th and 7th columns are attacking each other along a diagonal.
To implement the genetic algorithm approach, we need to transform a board configuration into a suitable input. In genetic algorithms, each member of a population is represented as a string over a limited set of symbols, much like a DNA sequence. We can encode the chessboard as a sequence of numbers, where the index of each number represents the column, and the number at each index represents the row, starting from the bottom left. The board shown above would be converted to 16257483. For this experiment, It represented each sequence as a list, such as [1, 6, 2, 5, 7, 4, 8, 3].
The diagram below provides an overview of how the genetic algorithm functions:
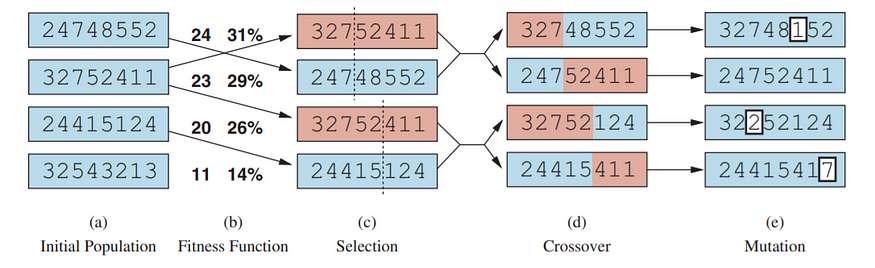
To begin, It initialized a random population of individuals with a POPULATION_SIZE set to 10. Next, It determined a fitness function that would simulate the "natural selection" mechanism of the algorithm. The most straightforward approach is to count the number of non-attacking queen pairs. The optimal solution to the problem would be 8 choose 2, representing the total possible number of queen pairs. In the code below, define NUM_QUEENS as 8.
def fitness_score(seq):
score = 0
for row in range(NUM_QUEENS):
col = seq[row]
for other_row in range(NUM_QUEENS):
# Queens cannot pair with themselves
if other_row == row:
continue
# Check if queens are in the same column
if seq[other_row] == col:
continue
# Check if queens are on the same diagonal
if other_row + seq[other_row] == row + col:
continue
if other_row - seq[other_row] == row - col:
continue
# Increment score if the pair of queens are non-attacking
score += 1
# Divide by 2 since pairs are symmetric (commutative)
return score / 2
Next comes the selection process. We define a mixing number, ρ, which represents the number of parents contributing to the creation of an offspring. Normally, ρ = 2. However, since this is a simulation, we can choose ρ > 2. For selecting parents, one approach is to randomly choose a number of individuals and then select the top ρ based on their fitness scores as parents. In this experiment, It limited the number of parents to half the population size and selected parents with a probability proportional to their fitness scores.
Afterward, we have the crossover phase. When ρ = 2, It randomly selected a crossover point (an index in the list). The first part of the first parent is combined with the second part of the second parent to create one offspring. This process is repeated for a second offspring. A visual example of this process is shown below:
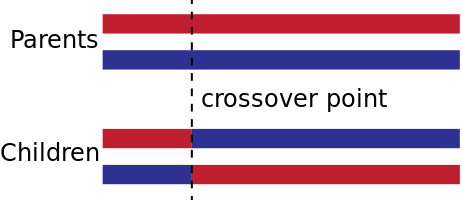
For instance, consider the parents 1234 and 5678 with a crossover point of 2. The resulting offspring would be 1278 and 3456.
To account for cases where ρ > 2, It modified the crossover approach as follows: generate ρ-1 random crossover points between [0, NUM_QUEENS]. Using these crossover points, we create offspring by mixing parts of ρ parents. Given x parents, we can generate x choose ρ * ρ! offspring. Below is the code implementing this crossover process, with MIXING_NUMBER = 2.
import itertools
def crossover(parents):
# Randomly select crossover points between parents
cross_points = random.sample(range(NUM_QUEENS), MIXING_NUMBER - 1)
offsprings = []
# Generate all permutations of parents
permutations = list(itertools.permutations(parents, MIXING_NUMBER))
for perm in permutations:
offspring = []
# Track the starting index for each parent section
start_pt = 0
# Loop through parents and crossover points (ignoring the last parent for now)
for parent_idx, cross_point in enumerate(cross_points):
parent_part = perm[parent_idx][start_pt:cross_point]
offspring.append(parent_part)
# Update starting point for the next parent
start_pt = cross_point
# Process the last parent's remaining segment
last_parent = perm[-1]
parent_part = last_parent[cross_point:]
offspring.append(parent_part)
# Flatten the offspring list
offsprings.append(list(itertools.chain(*offspring)))
return offsprings
Lastly, there’s the mutation step. For each element in the sequence, there’s a small probability, denoted by MUTATION_RATE = 0.05, that it will mutate to a different value.
def mutate(seq):
for row in range(len(seq)):
if random.random() < MUTATION_RATE:
seq[row] = random.randrange(NUM_QUEENS)
return seq
Using these functions, It tested the algorithm with the following parameters: POPULATION_SIZE = 10, NUM_QUEENS = 8, MIXING_NUMBER = 2, and MUTATION_RATE = 0.05. Below is the initial population from one test run:

When generating random populations, didn’t expect such high fitness scores. The highest score was 22, just 6 points away from the optimal score of 28. To check if this was simply luck, It generated 100,000 random board states and found an average fitness score of 20.13518 with a standard deviation of 2.3889. So, a fitness score of 22 is quite typical.
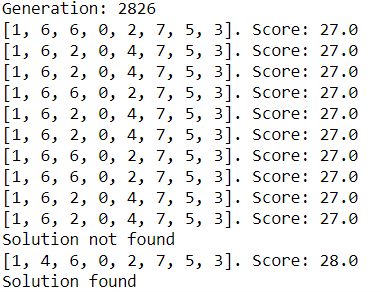
After running the algorithm, the solution was found in the 162nd generation. This was surprisingly quick, so It ran the algorithm again, and it took nearly 3000 generations. It suspect a favorable mutation or lucky recombination sped up the process in the first run.
In 200 runs of the algorithm, collected the following statistics: an average of 3813.53 generations with a standard deviation of 27558.146. The high standard deviation suggests something unusual occurred. The maximum number of generations was 377,241, and the minimum was just 10. It assume that the high-generation outlier occurred because some individuals had high fitness scores but lacked enough variety in their board configurations, leading the algorithm to rely on mutations to escape a local optimum.


By examining the results for the first and third quartiles, It noticed that the mean and standard deviation were more reasonable. When It applied an outlier removal function from Stack Overflow that filters data based on a distance of less than m=2 from the median, the statistics improved significantly.
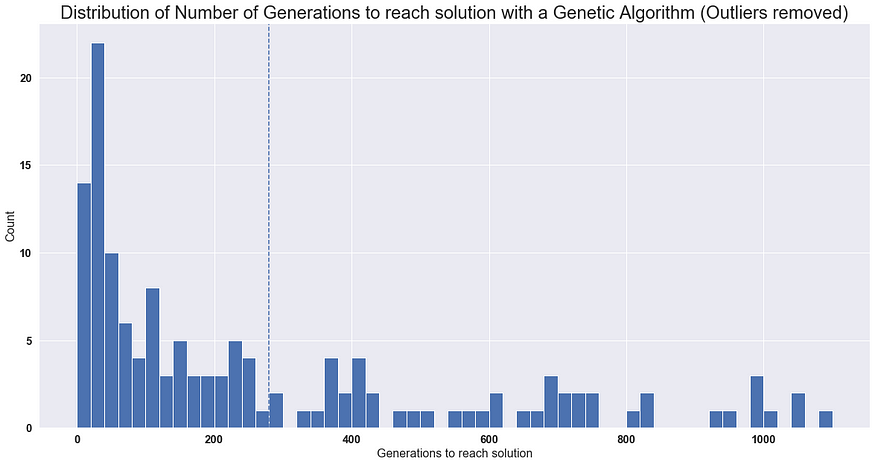
The dotted line represents the mean. If we consider a brute-force approach of randomly guessing the correct solution, the probability of finding the solution is approximately P(solution) = 0.0005. On average, it would take around 1386 generations for a 50% chance of guessing the solution, or 5990 generations for a 95% chance. Comparing this to the genetic algorithm's average of 280 generations, we see that the genetic algorithm is approximately 21 times faster.
Conclusion
A genetic algorithm can effectively solve the 8-Queens problem. While this experiment was a fun way to explore the genetic algorithm, don’t believe it’s the most efficient approach. A stochastic beam search, for example, might outperform it. Since recombination mixes board configurations in ways that often produce random offspring rather than “stronger” ones, there’s room for improvement. Further experimentation could include applying the algorithm to the N-Queens problem or increasing the mixing number to generate even more diverse offspring.
